A. Mengubah Sudut dari Derajat Desimal ke Derajat Menit Detik dan Sebaliknya
Secara umum, ada dua satuan dalam pengukuran sudut, yaitu satuan derajat (°) dan satuan radian (rad). Kita ketahui bahwa satu putaran penuh dengan arah perputaran berlawanan jarum jam adalah 360°. Dengan demikian jika busur lingkaran kita bagi menjadi 360 bagian yang sama, adalah 1°.
Untuk kepentingan ketelitian pengukuran suatu sudut, maka satuan derajat dibagi menjadi 60 bagian yang sama dan disebut menit. Sedangkan setiap menit dibagi lagi menjadi 60 bagian yang sama dan disebut detik. Simbol (‘) dan (“) berturut-turut digunakan untuk menyatakan ukuran sudut dalam satuan menit dan detik. Jadi,
1° = 60’ atau 1’ = (1/60)° dan
1’ = 60” atau 1” = (1/60)’ sehingga,
1° = 3600”
Dalam hal tertentu ukuran sudut dapat dinyatakan dalam bentuk desimal, misalnya
30’ = (30 x 1/60)° = 0,5°
Contoh:
Nyatakan 45,13° kedalam bentuk derajat menit detik!
Jawab:
Jawab:
45,13° = 45° + 0,13°
= 45° + (0,13 x 60)’
= 45° + (7,8)’
= 45° + 7’ + 0,8’
= 45° + 7’ + (0,8 x 60)”
= 45° + 7’ + 48”
= 45°7’48”
Jadi, 20,13° = 20°7’48”
Atau sebaliknya, kita sekarang akan mencoba mengubah satuan sudut dari bentuk derajat menit detik menjadi bentuk derajat desimal
Contoh:
Nyatakan 45°50’30” kedalam bentuk derajat desimal!
Jawab:
Jawab:
45°50’30” = 45° + 50′ + 30”
= 45° + 50′ + (30 x 1/60)’
= 45° + 50′ + 0,5′
= 45° + 50,5′
= 45° + (50,5 x 1/60)°
= 45° + 0,84°
= 45,84°
Jadi, 45°50’30” + 20,84°
B. Cara Menghitung Perbandingan Segmen Garis
Cara Menghitung Perbandingan Segmen Garis, Tanpa panjang lebar lagi yo check it out !
 |
| Gambar 1 |
Cara Menghitung Perbandingan Segmen Garis
Untuk cara menghitung perbandingan segmen garis bisa dilakukan dengan rumus perbandingan segmen garis, yaitu :
Rumus Perbandingan Segmen Garis :
Perhatikan gambar di atas !!!
Misalkan diketahui titik C berada di antara titi A dan titik B, sehingga : AC : CB = m : n, Maka Rumus perbandingan segmen garisnya :
AC : CB = m : n
AC : AB = m : (m + n)
CB : AB = n : (m + n)
Misalkan diketahui titik C berada di antara titi A dan titik B, sehingga : AC : CB = m : n, Maka Rumus perbandingan segmen garisnya :
AC : CB = m : n
AC : AB = m : (m + n)
CB : AB = n : (m + n)
Contoh Soal perbandingan segmen garis :
Jika panjang AB = 15cm, dan AP : PB = 2 : 3, tentukanlah panjang AP dan PB !!!
Penyelesaian soal perbandingan segmen garis :
Jawab :
Diketahui :
AB = 15
AP : PB = 2 : 3 = m : n
Ditanyakan :
AP = ???
PB = ???
Untuk menjawabnya kita gunakan rumus perbandingan segmen garis, maka :
Karena pada rumus sebagai titik tantara A dan B adalah C maka kita ganti dengan P karena pada soal titik P yang berada diantara titik A dan titik B :
AP : PB = 2 : 3
AP : AB = 2 : (2 + 3)
AP : AB = 2 : (2 + 3)
AP : AB = 2 : 5
PB : AB = 3 : (2 + 3)
PB : AB = 3 : 5
AP : 15cm = 2 : 5
AP/15cm = 2/5
(AP/15cm) x 15 = (2/5) x 15cm, (Kedua ruas dikali dengan 15 untuk menyederhanakan)
AP = 6cm
PB : 15cm = 3 : 5
PB/15cm = 3/5
(PB/15cm) x 15 = 3/5 x 15, (Kedua ruas dikali dengan 15 untuk menyederhanakan)
PB = 9cm
Jadi panjang AP dan PB adalah 6cm dan 9cm
Contoh Soal
Perhatikan gambar di bawah ini!

Jika panjang AC = 20 cm, BF = 4 cm, DF = 3,5 cm dan AB = 16 cm. Hitunglah panjang FG, DE, dan AD!
Penyelesaian:
Untuk mencari panjang FG gunakan perbandingan ∆BFG dengan ∆ABC, maka diperoleh:
AB:BF = AC:FG
Atau
AB/BF = AC/FG
16 cm/4 cm = 20 cm/FG
16 cm . FG = 20 cm . 4 cm
FG = 20 cm . 4 cm/16 cm
FG = 5 cm
Jadi panjang FG adalah 5 cm
Sekarang cari panjang DE dengan menggunakan perbandingan ∆BDE dengan ∆ABC, maka diperoleh:
DE : AC = BD:AB
atau
DE/AC=BD/AB (dalam hal ini BD = BF+DF = 7,5 cm)
DE/20 cm = 7,5 cm/16 cm
DE = 20 cm . 7,5 cm/16 cm
DE = 9,375 cm
Jadi panjang DE adalah 9,375 cm
Sekarang cari panjang AD dengan menggunakan konsep penjumlahan, yakni:
AB = AD + DF + BF
AB = AD + BD
AD = AB – BD
AD = 16 cm – 7,5 cm
AD = 8,5 cm
Jadi panjang AD adalah 8,5 cm.
C. Hubungan Antar Dua Garis dan Sudut yang Terbentuk
Hubungan Antar Dua Garis dapat berupa berpotongan, sejajar, berimpit, dan bersilangan. Sudut yang terbentuk akibat dua garis sejajar yang dipotong oleh sebuah garis dapat berupa sehadap, bertolak belakang, dalam bersebrangan, luar bersebrangan, sepihak, dan luar sepihak. Materi hubungan antara dua garis dan sudut yang terbentuk sering keluar di ujian nasional. Jadi, simak dengan baik materi mengenai hubungan antar dua garis dan sudut yang terbentuk.
Garis
Garis adalah kumpulan titik-titik yang banyaknya tak terhingga yang saling bersebelahan dan memanjang ke kedua arah. Hubungan antara dua garis dapat berupa sejajar, berpotongan, berimpit, dan bersilangan.
Berimpit
Jika semua titik pada sebuah garis terletak pada garis lainnya, atau sebaliknya, maka kedua garis tersebut dikatakan berimpit.
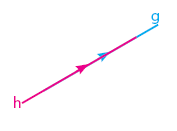
Dua Garis Sejajar
Karakteristik dua garis sejajar adalah kedua garis terletak pada satu bidang datar dan tidak mempunyai titik persekutuan (titik potong).
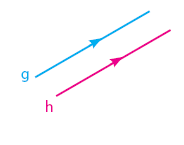
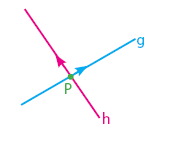
Berpotongan
Dua garis dikatakan berpotongan jika dua garis itu mempunyai satu titik persekutuan (titik potong).
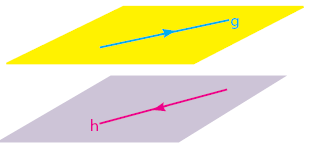
Dua Garis Bersilangan
Dua garis bersilangan jika kedua garis terketak pada bidang yang berbeda dan kedua garis tidak sejajar dan tidak berpotongan.
 Sudut
Sudut
Berimpit
Jika semua titik pada sebuah garis terletak pada garis lainnya, atau sebaliknya, maka kedua garis tersebut dikatakan berimpit.

Dua Garis Sejajar
Karakteristik dua garis sejajar adalah kedua garis terletak pada satu bidang datar dan tidak mempunyai titik persekutuan (titik potong).

Berpotongan
Dua garis dikatakan berpotongan jika dua garis itu mempunyai satu titik persekutuan (titik potong).

Dua Garis Bersilangan
Dua garis bersilangan jika kedua garis terketak pada bidang yang berbeda dan kedua garis tidak sejajar dan tidak berpotongan.
 Sudut
Sudut
Sebelum melanjutkan materi mengenai hubungan antar dua garis dan sudut yang terbentuk, mari kita mengenal sudut terlebih dahulu. Sudut adalah daerah yang dibatasi oleh dua sinar garis yang bertemu di satu titik pangkal. Perhatikan gambar sudut di bawah.
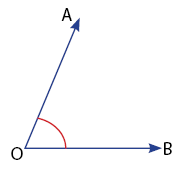
Keterangan:
O = titik pangkal
OA dan OB = kaki sudut
 = daerah sudut
= daerah sudut

Keterangan:
O = titik pangkal
OA dan OB = kaki sudut
Jenis-Jenis Sudut
Sudut Lancip 
Sudut Siku-Siku
Sudut Tumpul
Sudut Lurus
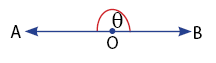
Sudut Refleks
C. Hubungan Antar Sudut

Sudut Siku-Siku

Sudut Tumpul

Sudut Lurus

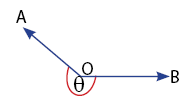
Sudut Refleks

C. Hubungan Antar Sudut
Komplemen dan Suplemen
Sudut komplemen dan penyiku yang akan dibahas merupakan lanjutan
Sudut Berpenyiku (Komplemen)
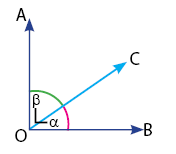
Sudut komplemen dan penyiku yang akan dibahas merupakan lanjutan
Sudut Berpenyiku (Komplemen)

Sudut Berpelurus (Suplemen)
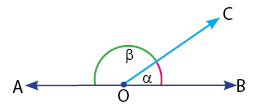
Sudut-Sudut yang Terbentuk Oleh Dua Garis Sejajar dan Dipotong Sebuah Garis
Perhatikan gambar di bawah!
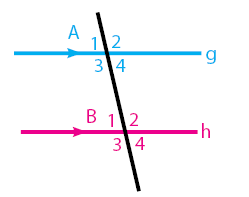
Sudut Sehadap
Karakteristik: Memiliki besar sudut yang sama
Perhatikan gambar di bawah!

Sudut Sehadap
Karakteristik: Memiliki besar sudut yang sama
Sudut Dalam Berseberangan
Karakteristik: Mempunyai besar sudut yang sama.
Karakteristik: Mempunyai besar sudut yang sama.
Sudut Luar Berseberangan
Karakteristik: Mempunyai besar sudut yang sama.
Sudut Bertolak Belakang
Karakteristik: Mempunyai besar sudut yang sama.
Karakteristik: Mempunyai besar sudut yang sama.
Sudut Luar Sepihak
Karakteristik: jumlah sudutnya
Contoh 1
Perhatikan gambar berikut!
Besar pelurus sudut KLN adalah ….
Besar pelurus sudut KLN adalah ….
Jumlah dua sudut yang saling berpelurus adalah 180o, maka:
Besar pelurus sudut KLN = besar sudut MLN
Contoh 2
Perhatikan gambar berikut!

Besar adalah ….
adalah ….

Besar
Cara 1:
Hitung besar ACB!
ACB!
Hitung besar
Selanjutnya hitung nilai x melalui segitiga ACB. Perhatikan 
INGAT!!! Jumlah ketiga sudut pada segitiga adalah .
.
INGAT!!! Jumlah ketiga sudut pada segitiga adalah
Besar
Cara 2:
Cari nilai x dengan rumus cepat berikut!
Cari nilai x dengan rumus cepat berikut!
Besar
VIDEO TURIAL GARIS &SUDUT
berikut sebagian tutorial materi garis dan sudut:
UJI KOMPETENSI GARIS DAN SUDUT
Kerjakan secara online dan mandiri


saya tdk terlalu paham pak...
BalasHapusMhn Maaf pak, form uji kompetensinya kok nggak bisa dibuka ya
BalasHapusiya, sedang diperbaiki lagi.
BalasHapusnanti dicoba lagi
sekarang dicoba lagi ya. perhatikan batasan waktunya
BalasHapusMohon maaf pak ini pilihan kelasnya kok cuman kelas 7H, I, J, A
BalasHapusKelas defg belum. Insya allah nanti malam ya saya isikan
BalasHapusMohon maaf pak utk kelas 7f dan 7g, masih belum ada pak
HapusTerimakasih...
Mohon maaf pak, kelas 7B sama 7C kok belum ada ya di form uji kompetensi
BalasHapusMohon maaf pak kelas 7f dan 7g kok tidak ada di form uji komp
BalasHapusMohon maaf pak kelas G kok gk ada pak
BalasHapusMohon maaf pak kelas 7G kok gak ada pak
BalasHapus