Ringkasan Materi
MENGENAL SEGITIGA
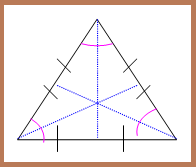
1. Segitiga Samasisi
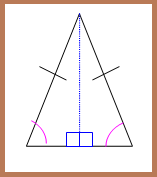
2. Segitiga Samakaki
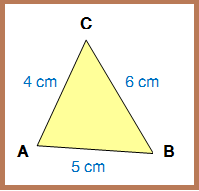
3. Segitiga Sebarang
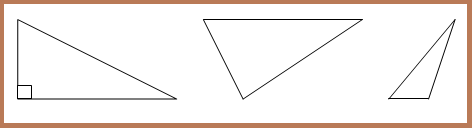
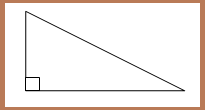
1. Segitiga Siku-Siku
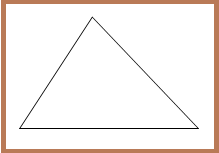
2. Segitiga Lancip
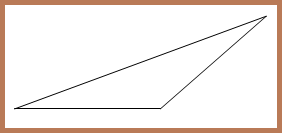
3. Segitiga Tumpul
Contoh Soal:
Contoh Soal:
1. Pada gambar di bawah ini, ∠A = 55°, ∠B = 60°. Tentukanlah besar ∠C.
Penyelesaian:
∠A + ∠B + ∠C = 180°
55° + 60° + ∠C = 180°
115° + ∠C = 180°
∠C = 180° – 115°
= 65°
55° + 60° + ∠C = 180°
115° + ∠C = 180°
∠C = 180° – 115°
= 65°
2. Pada gambar di bawah, besar ∠A = 2x, ∠B = x, ∠C = 3x. Hitunglah besar sudut-sudut tersebut?
Penyelesaian:
∠A + ∠B + ∠C = 180°
2x + x + 3x = 180°
6x = 180°
x = 30°
∠A + ∠B + ∠C = 180°
2x + x + 3x = 180°
6x = 180°
x = 30°
∠A = 2x ∠B = x ∠C= 3x
= 2 × 30° = 30° = 3 × 30°
= 2 × 30° = 30° = 3 × 30°
= 60° = 90°
APA ITU GARIS ISTIMEWA PADA SEGITIGA?
Dalam sebuah segitiga, terdapat empat buah garis istimewa yang sudah sangat dikenal. Garis-garis istimewa tersebut yaitu garis tinggi, garis bagi, garis berat serta garis sumbu. Berikut ini pembahasan lengkap dari garis-garis istimewa pada segitiga.
1. Garis Tinggi Segitiga
Garis tinggi merupakan sebuah garis yang ditarik dari satu titik sudut sebuah segitiga serta tegak lurus terhadap sisi depannya.
Perhatikan gambar segitiga ABC diatas, CS merupakan garis tinggi dari segitiga ABC. Karena CS merupakan garis yang ditarik dari satu titik sudut segitiga dan tegak lurus sisi depannya.
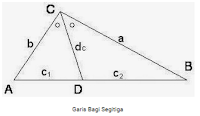
2. Garis Bagi Segitiga
Garis bagi merupakan garis yang ditarik dari suatu titik sudut sebuah segitiga dimana garis bagi akan membagi dua sama besar sudut tersebut.
Perhatikan segitiga ABC diatas, manakah yang disebut dengan rais bagi ? garis CD merupakan garis bagi segitiga.
3. Garis Berat Segitiga
Garis berat merupakan garis yang ditarik dari titik sudut sebuah segitiga yang membagi dua sama panjang sisi depannya.
Perhatikan segitiga ABC diatas, garis CD merupakan garis berat dari segitiga ABC diatas.
4. Garis Sumbu Segitiga
Garis sumbu merupakan garis yang ditarik tegak lurus pada suatu sisi yang membagi dua sama panjang sisi segitiga tersebut.
Setelah temen-temen perhatikan segitiga KLM diatas, tentunya temen-temen sudah tahu mana yang termasuk garis sumbu. Sebuah garis yangtegak lurus KM serta membagi KM menjadi dua bagian yang sama panjang itulah yang disebut garus sumbu.
RUMUS LUAS DAN KELILING SEGITIGA













pak soal uji kopetensi nya kok ga da?
BalasHapuskamu coba lagi setelah sahur
BalasHapusSaya sudah sangat faham pak
BalasHapus