MENYELESAIKAN PTLSV

QUIZ

MENYELESAIKAN PLSV

MENYEDERHANAKAN PECAHAN ALJABAR

Bagaimana Cara Menyederhanakan Pecahan Bentuk Aljabar?

Suatu pecahan bentuk aljabar dikatakan paling sederhana apabila pembilang dan penyebutnya tidak mempunyai faktor persekutuan kecuali 1, dan penyebutnya tidak sama dengan nol. Untuk menyederhanakan pecahan bentuk aljabar dapat dilakukan dengan cara membagi pembilang dan penyebut pecahan tersebut dengan FPB kedunya

KUIS

OPERASI HITUNG BENTUK ALJABAR

1. PENGURANGAN

contoh 1: Kurangkan (3x - 3y) dari (6x + y) ​

Jawab

   (6x + y) - (3x - 3y)

= 6x + y - 3x + 3y

= 3x + 4y

Jadi, (6x + y) - (3x - 3y) = 3x + 4y

contoh 2 : kurangkan : 5×-5y-6 oleh 4y-3×+8​

Jawab

  (5x-5y-6)-(4y-3x+8)

=5x-5y-6-4y+3x-8

=5x+3x-5y-4y-6-8

=8x-9y-14

2.PERKALIAN

Contoh:

Tentukan hasil perkalian bentuk aljabar berikut dalam bentuk jumlah atau selisih.

1. (2x + 3)(3x – 2)

2. (–4a + b)(4a + 2b)

3. (2x – 1)(x2 – 2x + 4)

4. (x + 2)(x – 2)

Penyelesaian:

1. (2x + 3)(3x – 2) kita selesaian dengan dua cara, yaitu sebagai berikut.

● Cara (1) dengan sifat distributif

(2x + 3)(3x – 2) = 2x(3x – 2) + 3(3x – 2)

= 6x2 – 4x + 9x – 6

= 6x2 + 5x – 6

● Cara (2) dengan skema

= 2x × 3x + 2x × (–2) + 3 × 3x + 3 × (–2)

= 6x2 – 4x + 9x – 6

= 6x2 + 5x – 6

2. (2x – 1)(x2 – 2x + 4) kita selesaikan dengan dua cara, yaitu sebagai berikut.

● Cara (1) dengan sifat distributif

(2x – 1) (x2 – 2x + 4) = 2x(x2 – 2x + 4) – 1(x2 – 2x + 4)

= 2x3 – 4x2 + 8x – x2 + 2x – 4

= 2x3 – 4x2 – x2 + 8x + 2x – 4

= 2x3 – 5x2 + 10x – 4

● Cara (2) dengan skema

= 2x × x2 + 2x × (–2x) + 2x × 4 + (–1) × x2 + (– 1) × (–2x) + (–1) × 4

= 2x3 – 4x2 + 8x – x2 + 2x – 4

= 2x3 – 4x2 – x2 + 8x + 2x – 4

= 2x3 – 5x2 + 10x – 4

Menyatakan bentuk perkalian menjadi bentuk penjumlahan seperti tersebut di atas disebut menjabarkan atau menguraikan. Amatilah contoh soal nomor 4 di atas. Apakah kalian sepakat bahwa secara umum bentuk perkalian (x + a)(x – a) = x2 – a2? Diskusikan hal tersebut dengan temanmu.

2.PEMBAGIAN

VIDEO PEMBAGIAN BENTUK ALJABAR

QUIZ

MENGENAL BENTUK ALJABAR

Bentuk Aljabar

Ilustrasi
Jumlah uang Tono 1000 lebih kecil dibanding dengan uang Sari. Jika kita sebuh uang sari sebagai x maka uang tono dapat dinyatakan dengan x – 1000. Jika kemudian diketahui jumlah uang sari adalah 3.000 maka uang tono adalah 3000 – 1000 = 2000.

Bentuk x-1000 dalam ilustrasi di atas dinamakan aljabar. Bentuk alajbar merupakan bentuk kalimat matematika yang terdiri dari huruf-huruf yang mewakili bilangn yang belum diketahui dengan menggunakan keterkaitan dengan bilangan lain. Contoh lagi, umur kaka 10 tahun lebih tua dari 2 kali umur adik. Jika kita misalkan umur adik adalah x maka umur kaka bisa ditulis dengan 2x + 10.

Bentuk aljbar sangat beraneka ragam, mulai dari yang sangat sederhana hingga yang paling rumit. Ada yang bentuk kuadrat, ada yang pecahan, dan ada yang bentuk pangkat tiga.

Unsur-Unsur Aljbar

Sebuah aljabar terdiri dari 4 bagian utama masing masing yakni variabel, konstanta, koefisien, dan faktor. Perhatikan bentuk aljabar berikut:

Unsur-unsur Aljabar

Bentuk aljabar adalah bentuk matematika yang didalamnya memuat variabel atau konstanta. Dalam aljabar terdapat beberapa istilah yang penting yaitu variabel, koefisien dan konstanta. Untuk lebih jelasnya perhatikan bentuk-bentuk aljabar berikut!

(i) 2x

(ii) -3q + 5

Keterangan :

(i) x disebut dengan variabel, 2 disebut dengan koefisien

(ii) q disebut dengan variabel, -3 disebut dengan koefisien dan 5 disebut dengan konstanta

Jadi, apa itu variabel, koefisien dan konstanta??

b. Suku-suku Sejenis

Suku sejenis adalah suku yang mempunyai variabel dan pangkat yang sama.

Contoh :

(i) 2 dengan 3 merupakan suku sejenis

(ii) -2pq dengan 4pq merupakan suku sejenis

(iii) 6x² dengan -3x² merupakan suku sejenis

Contoh soal:  Sederhanakan bentuk dari 5a - 2b + 6a +4b - 3c

5a - 2b + 6a + 4b - 3c

= 5a + 6a - 2b + 4b - 3c

= (5 + 6)a + (-2 + 4)b - 3c

= 11a + 2b - 3c

Penjumlahan

Dua bentuk aljabar dapat dijumlahkan apabila kedua bentuk aljabar itu sejenis. Perhatikan contoh berikut!

2a – 3b + 7 + a – 4b – 2

= (2a + a)+(-3b – 4b)+(7 – 2)

= 3a – 7b + 5

MATERI BERBENTUK VIDEO

QUIZ

Pembelajaran Digital materi Statistik

RINGKASAN MATERI

STATISTIKA (PENGENALAN DATA DAN PENYAJIAN DATA)

• Statistik adalah kumpulan fakta berbentuk angka yang disusun dalam daftar atau tabel, yang menggambarkan suatu persoalan
• Statistika adalah cabang dari matematika yang mempelajari cara pengumpulan, penyajian, penganalisaan, dan penarikan kesimpulan dari data.

A.  Pengenalan Data

     Data merupakan kumpulan keterangan atau informasi yang diperoleh dari hasil pengamatan suatu objek kemudian 

     disajikan secara jelas. Misalkan jumlah penduduk, jumlah siswa, tinggi badan siswa, dan berat badan siswa dan lain 

     sebaginya. Data dapat diperoleh melalui wawancara, angket, maupun observasi.

Pembelajaran Materi Segitiga

Ringkasan Materi

Dalam kehidupan sehari-hari, kamu dapat menemukan berbagai macam bentuk ataupun bangun, mulai dari yang sederhana seperti segitiga, segiempat, lingkaran, sampai dengan bangun yang rumit. Pada topik ini, kamu akan mempelajari sifat dari salah satu bangun tersebut, yaitu segitiga. Yuk simak dengan saksama.

MENGENAL SEGITIGA

Segitiga adalah bangun datar yang memiliki tiga sisi dan tiga sudut.

Sebuah segitiga biasa disingkat ∆.

Coba kamu perhatikan bangun segitiga berikut

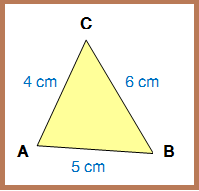Segitiga tersebut dinamai ∆ABC karena titik-titik sudutnya A, B, dan C, sedangkan sisi-sisinya AB, BC, dan AC. Panjang sisi-sisi tersebut adalah AB = 5 cm, BC = 6 cm, dan AC = 4 cm.

Pembelajaran Sifat, keliling dan Luas Segiempat

A. Ringkasan Materi

Bangun datar dapat didefinisikan sebagai bangun yang rata yang mempunyai dua demensi yaitu panjang dan lebar, tetapi tidak mempunyai tinggi atau tebal

Berdasarkan pengertian tersebut dapat ditegaskan bahwa bangun datar merupakan bangun dua dimensi yang hanya memiliki panjang dan lebar, yang dibatasi oleh garis lurus atau lengkung

Pembelajaran Materi Garis dan Sudut

Ringkasan Materi

A. Mengubah Sudut dari Derajat Desimal ke Derajat Menit Detik dan Sebaliknya

Secara umum, ada dua satuan dalam pengukuran sudut, yaitu satuan derajat (°) dan satuan radian (rad). Kita ketahui bahwa satu putaran penuh dengan arah perputaran berlawanan jarum jam adalah 360°. Dengan demikian jika busur lingkaran kita bagi menjadi 360 bagian yang sama, adalah 1°.

Untuk kepentingan ketelitian pengukuran suatu sudut, maka satuan derajat dibagi menjadi 60 bagian yang sama dan disebut menit. Sedangkan setiap menit dibagi lagi menjadi 60 bagian yang sama dan disebut detik. Simbol (‘) dan (“) berturut-turut digunakan untuk menyatakan ukuran sudut dalam satuan menit dan detik. Jadi,

1° = 60’ atau 1’ = (1/60)° dan

1’ = 60” atau 1” = (1/60)’ sehingga,

1° = 3600”

Dalam hal tertentu ukuran sudut dapat dinyatakan dalam bentuk desimal, misalnya

30’ = (30 x 1/60)° = 0,5°

Contoh:

Nyatakan 45,13° kedalam bentuk derajat menit detik!
Jawab:

45,13° = 45° + 0,13°

            = 45° + (0,13 x 60)’

            = 45° + (7,8)’

            = 45° + 7’ + 0,8’

            = 45° + 7’ + (0,8 x 60)”

            = 45° + 7’ + 48”

            = 45°7’48”

Jadi, 20,13° = 20°7’48”

Atau sebaliknya, kita sekarang akan mencoba mengubah satuan sudut dari bentuk derajat menit detik menjadi bentuk derajat desimal

Contoh:

Nyatakan 45°50’30” kedalam bentuk derajat desimal!
Jawab:

45°50’30” = 45° + 50′ + 30”

                  = 45° + 50′ + (30 x 1/60)’

                  = 45° + 50′ +  0,5′

                  = 45° + 50,5′

                  = 45° + (50,5 x 1/60)°

                  = 45° + 0,84°

                  = 45,84°

Jadi, 45°50’30” + 20,84°

B. Cara Menghitung Perbandingan Segmen Garis

    Cara Menghitung Perbandingan Segmen Garis, Tanpa panjang lebar lagi yo check it out !

Gambar 1

Cara Menghitung Perbandingan Segmen Garis

Untuk cara menghitung perbandingan segmen garis bisa dilakukan dengan rumus perbandingan segmen garis, yaitu :

Kisi-Kisi USBN-BK dan UNBK 2019 Jenjang SMP

Assalamualaikum Wr. Wb.
Diinformasikan kepada seluruh Siswa SMP Negeri 1 Gresik. kami sampaikan berikut adalah Kisi-Kisi Soal USBN-BK dan UNBK tahun pelajaran 2018/2019.

1. Kisi-Kisi USBN-BK. Download
2. Kisi-Kisi UN-BK. Download
3. Kisi-Kisi USBN-BK Bernomor. Download
Demikian informasi yang dapat kami sampaikan. terima kasih.
Wassalamualaikum Wr. Wb.

Hasil tryout MKKS 2019

20500492 Smp Negeri 1 Gresi... by on Scribd

JADWAL DAN PEMBAGIAN SESI TRYOUT MKKS SMP TAHUN 2018/2019

A.  JADWAL TRYOUT MKKS SMP KAB GRESIK
      TAHUN PELAJARAN 2018/2019

B. PEMBAGIAN SESI

Penyebaran Tryout Mkks Smp by on Scribd