BAHAN AJAR : POLA BILANGAN, BARISAN DAN DERET BILANGAN
Indikator :
1. Menyatakan masalah sehari-hari yang berkaitan dengan barisan dan deret bilangan
2. Menyebutkan unsur – unsure barisan dan deret seperti suku pertama, suku berikutnya, beda dan ratio.
A. Pola bilangan
Perhatikan pola gambar berikut !
Jika ditulis dalam bilangan maka menjadi pola bilangan 1,3,5,7, . . .
Maka untuk urutan bilangan ke-6 dapat ditentukan yaitu 11, akerna pola tersebut memiliki beda atau selisih tetap 2.
Perhatikan pola bilangan berikut !
1,2,3,5,8, . . .
Dapatkah ditentukan urutan (suku) ke -6 pada pola tsb. ?
Kita harus mengamati setiap urutan pada pola tersebut, jika kita amati terlihat bahwa pola tersebut adalah
Menemukan pola dari perhitungan bilangan
Misal bilangan berurutan adalah a dan a+1, maka
(a+1)2 – a2 = a2 +2a+1-a2
= 2a + 1
= (a + 1) + a
1. Tentukan hasil 42 – 32 = ( 4+ 1) + 4
= 5 + 4
= 9
2. Tentukan empat bilangan ganjil yang pertama 1+3+5+7 = . . .
“jumlah n bilangan ganjil yang pertama adalah kuadrat dari bilangan n “
Jawab : n2 = 42 = 16
B. Pola Bilangan Segitiga Pascal
Pola segitiga pascal adalah 1, 3, 6, 10, . . .
Penggunaan pola segitiga pascal untuk menentukan koefesien pada suku banyak (x+y)n dengan n bilanga asli.
( x+y) = 1x + 1y
(x+y)2 = 1x2 + 2xy + 1y2
(x+y)3 = 1x3+3x2y +3xy2+1y3
(x+y)4 = 1x4 +4x3y +6x2y2+4xy3 + 1y4
C. Barisan dan deret Bilangan
Terdapat dua macam bilangan deret bilangan berdasarkan atas banyaknya suku yaitu :
1. Deret berhingga
Adalah deret yang banyak sukunya terbatas
Misal : 1+2+3+4+ . . .+ 40 ditulis U1+ U2+ U3+ U4+. . .+ U40
2. Deret tak hingga
Adalah deret yang banyak sukunya tak terbatas
Misal : U1+ U2+ U3+ U4+. . .

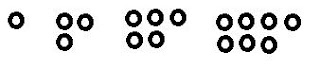

Tidak ada komentar:
Posting Komentar